Partial Differential Equations (PDEs) describe phenomena with multiple variables, offering incomplete solutions;
accessing PDEs in PDF format aids comprehensive study and practical application․
What are Partial Differential Equations?
Partial Differential Equations (PDEs) are mathematical equations involving unknown multi-variable functions and their partial derivatives․ Unlike Ordinary Differential Equations (ODEs) dealing with single independent variables, PDEs model scenarios with changes across space and time․ These equations are fundamental in describing a vast array of physical phenomena, from heat flow and wave propagation to fluid dynamics and quantum mechanics․
Understanding PDEs often requires exploring numerous solved examples and theoretical frameworks, making PDEs in PDF format invaluable resources․ These documents frequently contain detailed derivations, step-by-step solutions, and illustrative applications․ Accessing these PDF materials allows for self-paced learning and deeper comprehension of complex concepts, supplementing traditional textbooks and lectures․ They provide a readily available and portable means to study this crucial branch of mathematics․
Why Study PDEs? ⎯ Applications & Importance
Partial Differential Equations (PDEs) are crucial for modeling real-world phenomena across diverse fields; Engineering utilizes them for structural analysis, fluid flow simulations, and electromagnetic wave propagation․ Physics relies on PDEs to describe quantum mechanics, thermodynamics, and gravitational fields․ Even finance employs PDEs for option pricing models․
Mastering PDEs unlocks the ability to analyze and predict complex systems․ Accessing comprehensive resources, such as PDEs in PDF format, is vital for effective learning․ These PDF documents often present practical applications alongside theoretical foundations, bridging the gap between abstract concepts and real-world problems․ Studying PDEs empowers innovation and problem-solving in numerous disciplines, making them a cornerstone of scientific and technological advancement․

Fundamental Concepts
PDEs involve independent variables, dependent variables, order, and linearity; understanding these concepts is key when studying PDEs in PDF form․
Independent and Dependent Variables
Partial Differential Equations (PDEs) fundamentally rely on distinguishing between independent and dependent variables․ Independent variables, like time (t) and spatial coordinates (x, y, z), are freely chosen and serve as inputs to the equation․ Conversely, dependent variables, such as temperature (u) or displacement (w), are functions of these independent variables – their values depend on the chosen inputs․
Understanding this distinction is crucial when analyzing PDEs in PDF documents․ The notation u(x, t) clearly indicates that ‘u’ is dependent on ‘x’ and ‘t’․ PDF resources often showcase how manipulating these variables allows for the derivation of solutions․ Recognizing which variables you can control and which are outcomes is paramount for interpreting and applying PDE solutions found within PDEs in PDF format, enabling effective problem-solving and modeling of real-world phenomena․
Order and Linearity of PDEs
Partial Differential Equations (PDEs) are categorized by their order and linearity; The order of a PDE is determined by the highest derivative present within the equation․ For example, an equation containing a second-order derivative is a second-order PDE․ Linearity refers to whether the equation satisfies the superposition principle – meaning the sum of two solutions is also a solution․
When studying PDEs in PDF format, identifying these characteristics is vital․ Linear PDEs are generally easier to solve than nonlinear ones․ PDEs in PDF resources often classify equations based on these properties, aiding in solution strategy selection․ Understanding order and linearity helps in recognizing appropriate solution techniques and interpreting the behavior of the system modeled by the equation, as detailed in comprehensive PDEs in PDF guides․
Boundary and Initial Conditions
Partial Differential Equations (PDEs) rarely have unique solutions without additional information․ Boundary conditions specify the value of the solution (or its derivatives) on the boundary of the domain․ Initial conditions, crucial for time-dependent problems, define the solution at a specific initial time․
Analyzing PDEs in PDF materials emphasizes the importance of correctly applying these conditions․ Incorrectly specified conditions lead to inaccurate or non-physical solutions․ PDEs in PDF examples often demonstrate how different boundary and initial conditions affect the solution’s behavior․ Accessing detailed explanations within PDEs in PDF resources is essential for mastering this aspect, ensuring realistic and meaningful results from mathematical models․
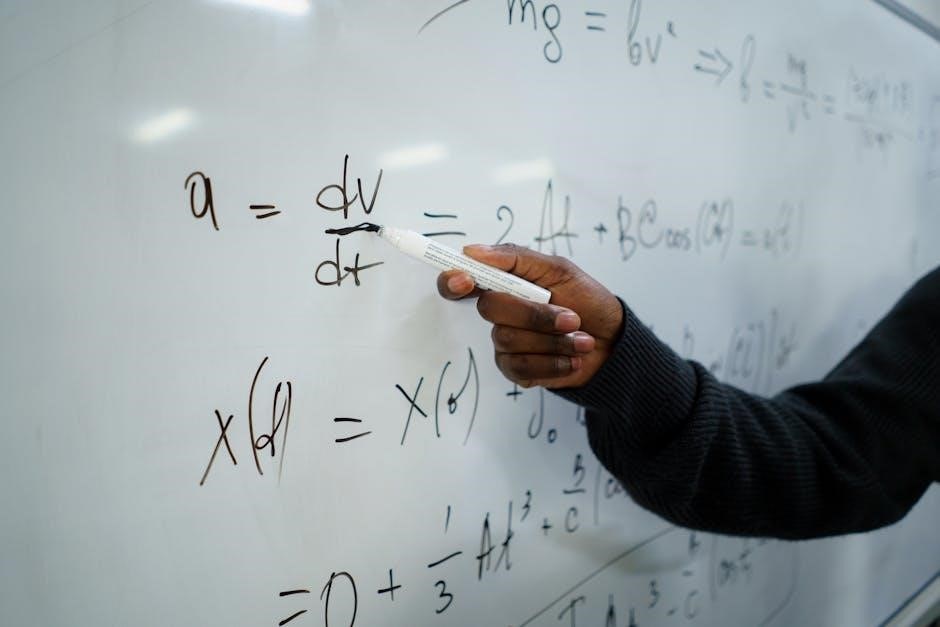
Common PDE Types & Their Characteristics
PDEs in PDF resources detail heat, wave, and Laplace’s equations, showcasing diffusion, propagation, and steady-state phenomena; understanding these is crucial for application․
The Heat Equation ⎯ Diffusion Processes
The Heat Equation, a cornerstone of PDEs, models how temperature distributes over time in a given region․ Numerous PDF resources comprehensively explain its derivation and solutions, detailing concepts like thermal diffusivity and boundary conditions․ These documents often present analytical solutions for simple geometries, alongside numerical methods for complex scenarios․
Understanding diffusion processes, from heat transfer in solids to the spread of pollutants in fluids, relies heavily on mastering this equation․ PDF guides frequently include worked examples illustrating applications in engineering and physics․ They also cover techniques like separation of variables and Fourier series, essential for solving the heat equation analytically․ Accessing these PDF materials provides a robust foundation for tackling real-world problems involving heat transfer and related diffusion phenomena․
The Wave Equation ⎯ Wave Propagation
The Wave Equation governs the propagation of waves – sound, light, water, and more – and is a fundamental PDE․ Numerous PDF resources detail its derivation, exploring concepts like wave speed, amplitude, and wavelength․ These documents often present solutions using techniques like d’Alembert’s formula and Fourier analysis, crucial for understanding wave behavior․
Studying wave propagation requires a firm grasp of this equation, and readily available PDF guides offer detailed explanations and practical examples․ They cover boundary conditions, initial conditions, and various methods for solving the equation analytically and numerically․ Accessing these PDF materials provides a strong foundation for analyzing diverse wave phenomena in physics and engineering, from vibrations in strings to electromagnetic radiation․
Laplace’s Equation ⎯ Steady-State Phenomena
Laplace’s Equation describes steady-state conditions, where quantities don’t change over time – think temperature distribution or electrostatic potential․ Finding solutions often involves techniques like separation of variables, and numerous PDF resources comprehensively explain these methods․ These documents detail boundary value problems, crucial for real-world applications․
Accessing PDE solutions in PDF format allows for in-depth study of these steady-state scenarios․ They showcase how Laplace’s equation models diverse phenomena, from heat flow in a solid object to fluid dynamics․ Detailed examples and step-by-step derivations within these PDF guides enhance understanding․ Mastering this equation, aided by readily available resources, is vital for engineers and physicists․
Methods for Solving PDEs
Solving PDEs utilizes techniques like separation of variables and Fourier transforms; numerous PDF guides detail these methods, offering step-by-step solutions and examples․
Separation of Variables
Separation of Variables is a powerful technique for solving Partial Differential Equations (PDEs), transforming a complex problem into simpler, ordinary differential equations․ This method assumes the solution can be expressed as a product of functions, each dependent on a single independent variable․ Numerous PDF resources comprehensively explain this approach, detailing its applicability to various PDE types like the heat and wave equations․
These PDF guides often include worked examples, illustrating how to correctly separate variables and solve the resulting ordinary differential equations․ Understanding the underlying assumptions and limitations of this method is crucial, and PDF materials frequently address these nuances․ Successfully applying separation of variables requires careful consideration of boundary conditions, which are also thoroughly covered in available PDF documentation․
Fourier Series and Transforms
Fourier Series and Transforms are essential tools for analyzing and solving Partial Differential Equations (PDEs), particularly those defined on infinite or semi-infinite domains․ These techniques decompose functions into a sum of sinusoidal components, simplifying the solution process․ Extensive PDF resources detail the mathematical foundations and practical applications of these methods, offering step-by-step guidance․
Many PDF guides demonstrate how to utilize Fourier transforms to convert PDEs into algebraic equations, which are often easier to solve․ They also cover inverse transforms to obtain the solution in the original domain․ Understanding convergence criteria and the properties of Fourier transforms, as explained in these PDF materials, is vital for accurate results․ Accessing these PDF documents enhances comprehension and problem-solving skills․
Finite Difference Method
The Finite Difference Method (FDM) approximates solutions to Partial Differential Equations (PDEs) by replacing derivatives with finite difference quotients․ This numerical technique discretizes the domain into a grid and solves algebraic equations at each grid point․ Numerous PDF resources provide detailed explanations of various FDM schemes, including explicit and implicit methods, along with their stability and convergence properties․
These PDF guides often include practical examples and code implementations, demonstrating how to apply FDM to solve specific PDEs․ Understanding the concepts of truncation error and grid spacing, as detailed in these PDF materials, is crucial for obtaining accurate solutions․ Accessing these PDF documents facilitates a deeper understanding and practical application of the FDM․
Finite Element Method
The Finite Element Method (FEM) is a powerful numerical technique for solving Partial Differential Equations (PDEs)․ It divides a complex domain into smaller, simpler elements and approximates the solution within each element․ Extensive PDF documentation details the mathematical foundations of FEM, including variational formulations and shape functions․ These resources often showcase practical applications across diverse fields․
Numerous PDF guides offer step-by-step instructions for implementing FEM, covering mesh generation, element assembly, and solution of the resulting system of equations․ Accessing these PDF materials is vital for understanding the intricacies of FEM and its advantages over other methods․ Detailed PDF examples demonstrate how to tackle complex geometries and boundary conditions effectively․

Specific Techniques & Considerations
PDF resources detail advanced PDE techniques like Green’s functions and characteristic methods, crucial for nuanced solutions and stability analysis․
Characteristic Methods for First-Order PDEs
Characteristic methods offer a powerful technique for solving first-order partial differential equations (PDEs), transforming them into ordinary differential equations along specific curves – the characteristics․ PDF documents detailing this method often illustrate how these curves are determined by the PDE’s coefficients, effectively simplifying the problem․ These resources frequently showcase step-by-step solutions, demonstrating how initial and boundary conditions are applied along these characteristics to obtain a unique solution․
Understanding the geometric interpretation of characteristics is vital, and PDF guides often include visual representations․ Furthermore, these materials frequently address potential issues like the formation of shocks or discontinuities, providing insights into solution validity․ Accessing well-explained PDF tutorials and examples is crucial for mastering this technique and applying it to diverse physical problems․
Green’s Functions and Integral Representations
Green’s functions provide a fundamental tool for solving inhomogeneous partial differential equations (PDEs)․ They represent the response of a system to a point source, enabling the construction of solutions via integration․ Numerous PDF resources detail the derivation and properties of Green’s functions for various PDEs, like the Poisson equation․ These documents often emphasize the importance of satisfying boundary conditions when constructing the Green’s function․
Integral representations, utilizing Green’s functions, transform the PDE into an integral equation, often simplifying the solution process․ PDF guides frequently present practical examples, demonstrating how to apply these techniques to solve real-world problems․ Accessing comprehensive PDF materials is essential for understanding the theoretical foundations and practical applications of Green’s functions․
Numerical Stability and Convergence
When solving partial differential equations (PDEs) numerically, ensuring stability and convergence is paramount․ Instability leads to unbounded errors, rendering the solution meaningless․ Convergence guarantees the numerical solution approaches the true solution as the discretization refines․ Many PDF resources delve into the Von Neumann stability analysis, a key technique for assessing stability․
These PDF guides often present the CFL (Courant–Friedrichs–Lewy) condition, crucial for explicit time-stepping schemes․ Understanding convergence rates – how quickly the error decreases with mesh refinement – is also vital․ Comprehensive PDF materials detail various numerical methods and their associated stability and convergence properties, aiding in selecting appropriate techniques for specific PDEs․

Resources for Further Learning ౼ PDF Focus
PDEs are extensively documented in PDF format; online repositories, textbooks, and free eBooks offer accessible learning materials for deeper exploration and understanding․
Online PDE Resources & Repositories
Numerous online platforms provide access to valuable resources concerning Partial Differential Equations (PDEs), often available as downloadable PDF documents․ Websites like MIT OpenCourseWare and various university lecture note repositories frequently host complete courses, including problem sets and solutions, in PDF format․
Dedicated PDE websites and online communities offer curated collections of lecture notes, research papers, and solved examples․ Searching academic databases like arXiv․org can yield preprints and published articles related to specific PDE topics, typically accessible as PDFs․
Project Gutenberg and similar digital libraries sometimes contain older, foundational texts on differential equations, which can be downloaded as PDFs for historical context․ Remember to critically evaluate the source and author’s credentials when utilizing online PDF resources․
Recommended Textbooks (PDF Availability)
s․
s are typically behind a paywall, unofficial versions circulate․ Be mindful of copyright restrictions when downloading and using these resources․
Always prioritize legally obtained PDF versions when possible, supporting authors and publishers․ University libraries often provide access to digital textbooks, including PDE resources․
Free PDE eBooks and Lecture Notes (PDF)
Numerous universities offer Partial Differential Equations (PDE) lecture notes in PDF format freely available online․ MIT OpenCourseWare and similar platforms are excellent resources, providing complete course materials, including problem sets and solutions․ Websites dedicated to mathematical resources often curate collections of PDE related PDFs․
Project Gutenberg sometimes hosts older, out-of-copyright texts on differential equations․ Searching specifically for “PDE lecture notes PDF” yields a wealth of results, but quality varies․ Exercise caution when downloading from unfamiliar sources, verifying file safety․
Remember to critically evaluate the content and author’s credentials before relying on free PDF resources․

Advanced Topics
PDE research delves into nonlinearities and higher dimensions; finding relevant PDF resources requires specialized searches and access to academic databases for in-depth study․
Nonlinear PDEs
Nonlinear Partial Differential Equations (PDEs) present significant challenges due to the lack of general solution techniques, unlike their linear counterparts․ Their behavior can be incredibly complex, exhibiting phenomena like shock waves, solitons, and chaos․ Consequently, analytical solutions are often unattainable, necessitating reliance on numerical methods and approximations․
Accessing research papers and advanced texts in PDF format becomes crucial for understanding these intricacies․ These PDF resources often detail specific techniques like perturbation methods, variational approaches, and advanced numerical schemes tailored for nonlinear problems․ Furthermore, exploring PDF-based case studies reveals practical applications in diverse fields, including fluid dynamics, plasma physics, and financial modeling․ Careful evaluation of the source’s credibility is paramount when utilizing these PDF materials, ensuring the rigor and validity of the presented information․
PDEs in Higher Dimensions
Extending Partial Differential Equations (PDEs) to higher spatial dimensions (beyond two) dramatically increases complexity․ Analytical solutions become exceedingly difficult to obtain, often requiring sophisticated mathematical tools and computational resources․ The curse of dimensionality impacts numerical methods, demanding finer discretizations and increased computational cost․
Consequently, accessing specialized literature in PDF format is essential․ These PDF resources frequently present advanced techniques like multi-grid methods and domain decomposition strategies designed to handle the increased computational burden․ Exploring PDF-based research papers reveals applications in areas like atmospheric modeling, materials science, and complex fluid flows․ When utilizing these PDF materials, verifying the source’s authority and the validity of the presented methods is crucial for reliable results and understanding․
Applications in Engineering and Physics
Partial Differential Equations (PDEs) are foundational across numerous engineering and physics disciplines․ From modeling heat transfer in aerospace components to simulating fluid dynamics in civil engineering, their applications are vast․ In physics, PDEs describe wave propagation, quantum mechanics, and electromagnetism․
Accessing detailed case studies and solutions in PDF format is invaluable for practical application․ These PDF resources often contain real-world examples, boundary conditions, and numerical implementations․ Searching for PDEs related PDFs focused on specific engineering problems (e․g․, bridge stability, reactor design) provides targeted insights․ Critically evaluating the assumptions and limitations detailed within each PDF document ensures appropriate application and accurate interpretation of results․

Software Tools for PDE Solving
PDE solving software, like MATLAB and COMSOL, complements theoretical understanding; PDF documentation and tutorials are crucial for mastering these tools and applying PDE solutions․
MATLAB PDE Toolbox
MATLAB’s PDE Toolbox provides a finite element analysis (FEA) framework for solving various partial differential equations (PDEs)․ It’s exceptionally useful for modeling physical phenomena in one, two, or three spatial dimensions․ Users define the geometry, PDEs, boundary conditions, and mesh, then the toolbox solves the equations numerically․
A significant advantage is the availability of extensive documentation, often found as PDF manuals, detailing functions, examples, and tutorials․ These PDF resources are invaluable for learning the toolbox’s capabilities and troubleshooting issues․ The toolbox supports diverse PDE types, including elliptic, parabolic, and hyperbolic equations, making it versatile for numerous applications․ Furthermore, it integrates seamlessly with other MATLAB tools for visualization and post-processing of results․ Accessing example scripts and associated PDF guides accelerates the learning curve and enables efficient problem-solving․
COMSOL Multiphysics
COMSOL Multiphysics is a powerful simulation software adept at solving partial differential equations (PDEs) arising from coupled physics phenomena․ It employs the finite element method (FEM) to model complex systems in various disciplines, including electromagnetics, fluid dynamics, and heat transfer; Its strength lies in handling multiphysics problems where multiple PDEs interact․
Comprehensive documentation, frequently available as detailed PDF manuals, guides users through model creation, equation setup, and result analysis․ These PDF resources are crucial for mastering the software’s extensive features․ COMSOL allows defining custom PDEs and boundary conditions, offering flexibility for specialized applications․ The software’s user interface facilitates geometry creation and mesh generation․ Accessing application examples with accompanying PDF documentation provides practical insights and accelerates the learning process for solving intricate PDE-based problems․

Finding and Utilizing PDE PDFs
PDE PDFs offer accessible learning resources and solved problems; careful evaluation of source credibility is vital when utilizing partial differential equations PDF materials․
Searching for PDE Solutions in PDF Format
Locating PDF resources containing solutions to Partial Differential Equations (PDEs) requires strategic searching․ Utilize specific keywords like “PDE solutions PDF,” “solved PDEs,” or the equation name (e․g․, “Heat Equation PDF solutions”)․ Explore academic databases like JSTOR, ScienceDirect, and university repositories, often hosting theses and dissertations with detailed PDE analyses in PDF format․
Google Scholar is invaluable, filtering results to “PDF” format․ Be mindful of search operators; using quotation marks ensures exact phrase matches․ Websites dedicated to mathematical resources and engineering forums frequently link to relevant PDFs․ Remember to verify the source’s authority and the solution’s accuracy before relying on it for academic or professional purposes; A thorough search yields a wealth of partial differential equations PDF materials․
Evaluating the Credibility of PDF Sources
When utilizing Partial Differential Equations (PDEs) solutions found in PDF format, critical evaluation is paramount․ Assess the author’s credentials and institutional affiliation; academic publications and university-hosted materials generally offer higher reliability․ Scrutinize the document’s publication date, favoring recent sources reflecting current understanding․
Cross-reference solutions with established textbooks and reputable online resources to verify accuracy․ Be wary of PDFs lacking clear authorship or originating from unknown websites․ Look for logical consistency in the derivation and solution process․ A well-presented PDE PDF will demonstrate a clear methodology and acknowledge any assumptions made․ Prioritize sources demonstrating scholarly rigor and transparency․
